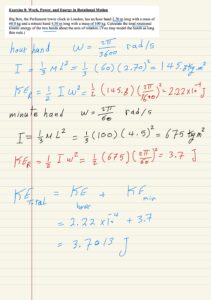rotational motion
The figure shows three small spheres that rotate about a vertical axis. The perpendicular distance between the axis and the center of each sphere is given. Rank the three spheres according to their rotational inertia about that axis, greatest first.
During a certain period of time, the angular position of a swinging door is described by 𝜃 = 4.00 + 8.00𝑡 + 3.00𝑡!, where 𝜃 is in radians and 𝑡 is in seconds. Determine the angular position, angular speed, and angular acceleration of the door at 𝑡 = 2.00s.
A rotating wheel requires 2.00 s to complete 15.0 revolutions. Its angular speed at the end of the 2.00-s interval is 85.0 rad/s. What is the constant angular acceleration of the wheel?
A wheel 1.80 m in diameter lies in a vertical plane and rotates with a constant angular acceleration of 3.00 rad/s2. The wheel starts at rest at 𝑡 = 0, and the radius vector of point P on the rim makes an angle of 30.0° with the horizontal at this time. At 𝑡 = 2.00 s, find (a) the angular speed of the wheel, (b) the linear speed and acceleration of the point P, and (c) the angular position of the point P.
The four particles in Figure are connected by rigid rods of negligible mass. The origin is at the center of the rectangle. If the system rotates in the xy plane about the z axis with an angular speed of 4.00 rad/s, calculate (a) the moment of inertia of the system about the z axis and (b) the rotational energy of the system.
Exercise 6: Torque
Find the net torque on the wheel in Figure about the axle through 𝑂 if 𝑎 = 5.0 cm and 𝑏 = 15.0 cm.
Exercise 7: Relationship Between Torque and Angular Acceleration
The combination of an applied force and a frictional force produces a constant total torque of 32.0 N.m on a wheel rotating about a fixed axis. The applied force acts for 5.00 s; during this time the angular speed of the wheel increases from 0 to 9.00 rad/s. Find (a) the moment of inertia of the wheel, (b) the number of revolutions of the wheel during this time period.
Exercise 8: Work, Power, and Energy in Rotational Motion
Big Ben, the Parliament tower clock in London, has an hour hand 2.70 m long with a mass of 60.0 kg and a minute hand 4.50 m long with a mass of 100 kg. Calculate the total rotational kinetic energy of the two hands about the axis of rotation. (You may model the hands as long thin rods.)